These are some fractals I have been working on recently. I’ve been very interested in fractals for at least a month; and I would like to show and explain some of the best things I have made using my newfound expertise.
Explanation
Before starting I would like to explain how I made these (hopefully) beautiful pictures. I used math.
If you want to skip past all the math and just see the pictures, go to the start of the ‘Pictures’ section.
If you would like to delve into the math, use this link:
https://en.wikipedia.org/wiki/Mandelbrot_set
If you want a quick explanation from me then keep reading.
(This explanation assumes that the reader knows about negative numbers and square roots.)
Using normal numbers, you cannot take the square root of a negative number. It has no real number solution. But what if you don’t limit yourself to real numbers? You can head into the realm of the complex, where √-1 = i, not a boring ‘undefined’. Then you can do math to i, and get a whole infinite sheet of complex numbers (the ‘Complex Plane’), containing things from ‘-i’ to ‘3+4i’. Using this, it is possible to do all sorts of interesting things.
One of these things is the Mandelbrot Set, named after Benoit B. Mandelbrot. The Mandelbrot Set looks like this:
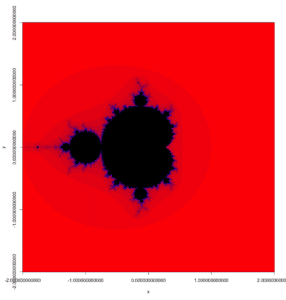
The Mandelbrot Set
I’m going to leave you to decide what you think of it. I think it’s beautiful; but I’m biased because I know what you get when you zoom in. And something interesting about the Mandelbrot set is that no matter how far you zoom in, you can always go further. This thing has infinite detail. This makes it a fractal, as that is literally the definition of a fractal – it has infinite detail.
The Mandelbrot Set is made like this:
Choose a complex number C. Then define a complex number Z to be zero. Next, set Z to be Z^2 + C. Then repeat, again and again and again. Keep repeating. If Z gets bigger than 2, then colour the point on the complex plane representing C red. If you’ve done this for a while, and Z has never got bigger than 2, then you should be safe in assuming that it never will. Colour the point representing C white. Do this for EVERY POINT IN THE COMPLEX PLANE, and you get the Mandelbrot Set.
But wait, I hear you saying. Some of your picture is blue!
Usually there is another step. If Z gets bigger than 2, then colour it in a spectrum based on how long it took. If it took only one iteration (repetition of Z^2 + C) then colour it red. If it only got bigger than 2 on the last iteration you did, colour it blue. If it was somewhere in the middle, colour it on a spectrum. For the picture above, the spectrum just gradually shifts from the starting colour (red) to the finishing colour (blue), but for all the other pictures there are other colours in between, which it gradually shifts to before moving to the final colour.
With that explained, we can now move on to…
Pictures
If you zoom in, then it looks REALLY COOL. So, I zoomed in.
Level 1
This contains the most tame things, nothing too amazing (but this is the Mandelbrot Set, most of these pictures will still be ‘Whoa’-worthy.)
The colour scheme I’m using for this section goes from magenta to black and then repeats that another 3 times. The addition of black earlier in the sequence creates a shadow effect.

Already, just zooming into the section on the left reveals this. But it isn’t enough.

Zooming into the left again. It doesn’t change much, but it does reveal a small blob slightly further to the left. So, without further ado, let’s zoom into that.

Now we’re getting somewhere. The blob is a smaller Mandelbrot Set. These ‘minibrots’ are dotted everywhere around the set and are the best way to create good pictures. We’ll come back to this minibrot (which happens to be the largest one) in the next section, but for now, we’re zooming into a different area.

The area to the right of the Mandelbrot Set is called a valley. There are more valleys, but this is the largest. Notice the interesting formations repeating themselves down into the abyss. We’re going to zoom into one of those next. But that should go in the next section.
Level 2
This section contains better stuff, but there is more yet to come, even after this. The colour scheme here is more upbeat, maybe to the point of being a bit fiery considering its use of red and orange, but I think that contrasts well with last section’s dark colour scheme.

Look at that! The intricate spirals, the beautiful patterns perfectly flowing into one another. Time to zoom in once again…

It’s now easier to see the minibrots. I can count 12 in this picture, but some are very small. (One is even a tiny little black dot!)

Getting closer to the larger minibrot, just slightly to the left of the centre. The intricate pattern surrounding it is now easily visible.

I said earlier I’d come back to the largest minibrot. Well, this is the largest valley of that minibrot. Notice the difference between it and the previously shown valley – the tendrils coming off of it. Zoom in further…

Now almost everything is blackness… So let’s zoom into the white region at the far right, and let’s zoom into it deep. Really deep.

Really, really deep. Now let’s zoom into that yellow formation towards the centre, and put the result in the next section.
Level 3
The absolute best I have.
I’ve switched to a colour scheme that is neither light nor dark. Just green.

This is one of my favourite areas in the whole Mandelbrot Set. Hopefully you can see why, and if not then the next picture should convince you.

I don’t have much other commentary on this apart from ‘YEAH!!!’ and I think the same will apply for the rest of the section. I will just say which area I’ve gone to and nothing else.

This is the small blob at the centre of the main formation. Spot the minibrot.

The small blob at the centre of the small blob at the centre of the main formation.

The minibrot at the centre of the small blob at the centre of the small blob at the centre of the small blob at the centre of the small blob at the centre of the small blob at the…
…; and also the end of the Mandelbrot Set Tour. I hope you liked it and I will make another one soon.
Recent Comments